Publié le : 29 janvier 20185 mins de lecture
- Définitions
- Vecteurs
- Translation d’un point
- Translation d’une figure
- Somme de deux vecteurs : Relation de Chasles
- Composée de deux translations
- Composée de deux symétries centrales
- Vecteurs et parallélogramme
- Définition vectorielle du parallélogramme
- Règle du parallélogramme
- Représentation de la somme
Définitions
Vecteurs
Deux points A et B pris dans cet ordre représentent un vecteur 
. On note 
=
: la translation qui transforme A en B est appelée translation de vecteur ou de vecteur .
Le vecteur est caractérisé par :
- sa direction qui est celle de la droite ( AB) ;
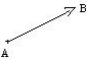
- son sens : de A vers B ;
- sa longueur : la longueur du segment [ AB].
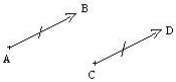
Égalité de deux vecteurs
On dit que deux vecteurs et 
sont égaux si :
- les droites ( AB) et ( CD) qui portent les vecteurs sont parallèles ;
- les longueurs sont égales : AB = CD ;
- les vecteurs ont même sens.
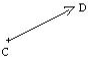
Translation d’un point
Soient le vecteur et le point C.
Le point D tel que = est le translaté du point C dans la translation de vecteur .
= signifie que D est l’image de C dans la translation de vecteur .
On dit que les vecteurs et sont colinéaires.
=
signifie que B est le milieu de [ AC].
Translation d’une figure
La figure F’ translatée de la figure F dans la translation de vecteur est superposable à la figure F :
c’est à dire qu’elle a les mêmes mesures que la figure F.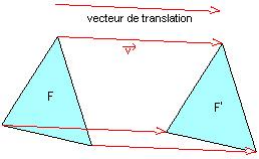 
Somme de deux vecteurs : Relation de Chasles
Soient deux vecteurs 
et et un point A
En A on trace le vecteur colinéaire au vecteur et en B, on trace le vecteur colinéaire au vecteur .
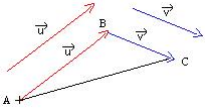
Les vecteurs et 
sont des vecteurs opposés, on a :
=- 
Le vecteur nul est un vecteur dont son origine et son extrémité sont confondues.
Simplifier la somme vect orielle : 
D’après la relation de Chasles on a : 
,
la somme devient : 
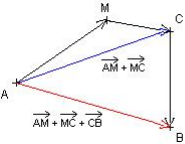
Or d’après la relation de Chasles 
, d’où :
=
Composée de deux translations
Effectuer la translation de vecteur suivie de la translation de vecteur revient à effectuer la translation de vecteur . 
La composée de deux translations est une translation dont le vecteur est la somme des vecteurs des deux translations.
Composée de deux symétries centrales
La symétrie de centre A suivie de la symétrie de centre B est équivalente à la translation de vecteur 2
Dans la symétrie de centre A, le point M a pour image le point M’.
Dans la symétrie de centre B, le point M’ a pour image le point M ».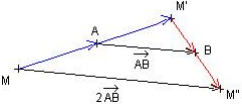 
Le point M a pour image le point M’ ‘ dans la translation de vecteur 2.
À découvrir également : Comment dessiner un cylindre ?
Vecteurs et parallélogramme
Définition vectorielle du parallélogramme
Si un quadrilatère ABCD est un parallélogramme alors =
Réciproquement : si un quadrilatère ABCD est tel que = alors ce quadrilatère est un parallélogramme.
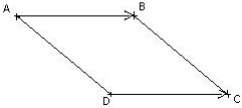
Règle du parallélogramme
Si ABCD est un parallélogramme alors 
Réciproquement : Soient quatre points non alignés A, B, C et D tels que alors ABCD est un parallélogramme et [ AC] est une diagonale.
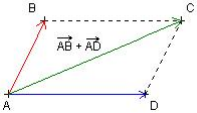
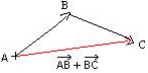
Représentation de la somme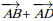 
Pour représenter le vecteur somme , il suffit de construire le parallélogramme ABCD.
On a alors : 
