Vecteurs et repères

Vecteurs

Définition

Représentation d'un vecteur

Une unité de longueur étant choisie dans le plan, un vecteur  est défini par sa direction (la droite (AB)  ), son sens (de A vers B) et sa longueur "norme de " notée  (distance AB).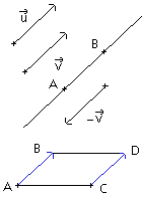                                

Egalité de deux vecteurs

Deux vecteurs égaux ont même direction, même sens et même norme : = ⇔ = Deux vecteurs de sens contraires ont même direction et même norme : =- ⇔ = Soient deux vecteurs égaux  et  alors = si et seulement si ABDC est un parallélogramme.

Addition de deux vecteurs

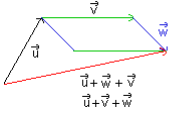
Relation de Chasles

+=                                                                                                            

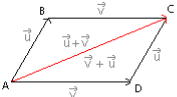
Règle du parallélogramme

+= [AC] est la diagonale du parallélogramme ABCD. Cas de deux vecteurs et de même direction                                                                                            

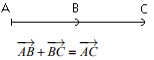
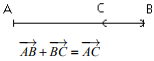
Propriétés de l'addition vectorielle

                                                                                           

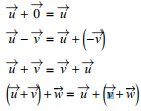
Multiplication par un nombre

Vecteurs colinéaires

On dit que les vecteurs  et   sont colinéaires colinéaires colinéaires s'il existe un réel k tel que =k  et  ont même direction, même sens si k > 0, sens opposé si k < 0 et on a == |k|.

Propriétés

• Soient les vecteurs  et 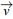  et les réels a et b on a :

a(+)=a+a ( a+b)=a+b a(b)= ab

• Si k= 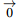 alors k =0 ou =
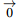
• Trois points A, B et C sont alignés si et seulement si les vecteurs 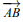 et 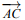 sont colinéaires.
• Soient les points A et B et un réel k, les points M tels que 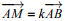 sont les points de la droite (AB).
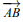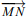• Deux droites (AB) et (MN) sont parallèles si et seulement si  et  sont colinéaires.

Applications

Milieu d'un segment Le point I est le milieu de [AB] si et seulement si  ou encore  ou encore  Centre de gravité Soit G le centre de gravité du triangle ABC alors on montre que  Expression vectorielle du théorème de thalès

Repères

Repère orthonormal et orthonormé

Dans le plan soit le point O, on pose .  On définit un repère orthonormal . Dans ce repère tout point M a pour coordonnées (x; y) où x est l'abscisse et y l'ordonnée :  De même le vecteur  de coordonnées  peut s'écrire 

Si la maille du quadrillage est carrée on a un repère orthonormé et un repère quelconque si la maille du quadrillage est un parallélogramme.

Calculs sur les coordonnées

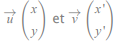Dans un repère soient les vecteurs  et  et les points A(x_A; y_A) et B(x_B; y_B) : Egalité de deux vecteurs Somme de deux vecteurs Multiplication par un réel Soit un réel k, alors  Coordonnées d'un vecteur Distance Milieu d'un segment Le milieu I de [AB] est  Vecteurs colinéaires Les vecteurs  sont colinéaires, si et seulement si xy' = yx'.