Racines carrées

Publié le : 29 janvier 20185 mins de lecture

Définition

L’écriture a p se lit « racine carrée de a « , elle désigne un nombre positif et n’a de sens que si a > 0.
Le symbole √ est appelé radical. Dans l’expression √a = x on a a > 0 et x > 0.

Si x = √a alors x² = a.
Pour a > 0 on a : (√a)² = a et √a² = a.
√a² existe même si a est négatif, mais on a √a² = a uniquement si a est positif.
Si a est négatif alors √a² = – a, en effet dans ce cas -a est positif.

À découvrir également : Puissances

Propriétés

Soient a et b deux nombres positifs : √(a×b) = √a × √b et pour b ≠ 0, 

Il n’existe aucune règle de calcul concernant la somme de deux racines carrées. √(a + b) ≠ √a + √b

Interprétation géométrique

Dans le triangle ABC rectangle en A tel que AB = AC = 1 on a, d’après le théorème de Pythagore :

BC² = AB² + AC², d’où BC² = 1² + 1² = 2, donc BC = √2.

Ordre des racines carrées et des carrés

Pour tout nombre positif a et b on a :
Si a² > b² alors a > b

Donc si a > b alors a p > b p .

et réciproquement :
Si a > b alors a² > b²
Donc si √a > √b alors a > b.

Résoudre une équation de la forme  x² = a

Si a > 0 alors l’équation x² = a a deux solutions √a et – √a.
Si a < 0 alors l’équation x² = a n’a pas de solution.
Si a = 0 alors l’équation x² = a devient x² = 0 et a une seule solution x = 0.

La touche  de la calculatrice

La touche  de la calculatrice a déjà été utilisée en classe de quatrième lors d’exercices portant sur le calcul de côtés d’un triangle rectangle à partir du théorème de Pythagore. Cette touche fournit une valeur approchée d’une racine carrée.

Calculs sur les radicaux

Ecrire √n sous la forme a√b

n, a et b sont des entiers et b est le plus petit possible.

Ecrire √45 sous la forme a√b avec b entier le plus petit possible. On écrit 45 sous la forme d’un produit d’un carré par un entier : 45 = 9×5
On a donc : √45 = √(9×5)
On sait que la racine carrée d’un produit est égale au produit des racines carrées, on a donc :
√45 = √9 × √5, soit √45 = 3 √5.

Simplifier une somme

n√b + p√b = ( n + p)√b

Seules les sommes ayant le même nombre sous le radical peuvent être simplifiées.

L’écriture 5√7 – 3√7 est simplifiable : 5√7 – 3√7= 2√7.

En revanche 2√5+ 4√3 ne l’est pas.

Rendre rationnel le dénominateur d’une fraction

Rendre rationnel le dénominateur d’une fraction c’est supprimer la racine du dénominateur de cette fraction.

• Soit la fraction 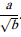. (b > 0)

En multipliant numérateur et dénominateur de cette fraction par b p on obtient la fraction équivalente :

On voit que le radical à « disparu » du dénominateur.

• Soit la fraction 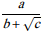 . (c > 0)

On multiplie le numérateur et le dénominateur par l’expression conjuguée du dénominateur : b – √c :

Ici aussi le radical à « disparu » du dénominateur.

Ecrire sans radical au dénominateur 

On multiplie le numérateur et le dénominateur par √2

Comparaison de nombres contenant des radicaux

Pour comparer deux expressions contenant des racines carrées il suffit de les élever au carré. En effet on a vu au paragraphe « Ordre des racines carrées et des carrés » que les nombres et leurs carrés sont rangés dans le même ordre.

Comparer 2√3 et 3√2

        On les élève au carré et on obtient :
(2√3)² = 12 et (3√2)²= 18
Or 12 < 18, donc : 2√3 < 3√2.