Pyramide
Caractérisation d'une pyramide
Une pyramide est régulière lorsque sa base est un polygone régulier et que sa hauteur [SO] passe par le centre O du plolygone de base.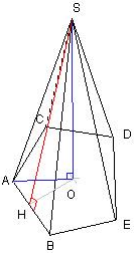 
(SO) est perpendiculaire à toute droite du plan contenant la base de la pyramide. Toutes les faces latérales sont des triangles isocèles superposables.
Eléments caratéristiques d'une pyramide
Longueur de l'arête
Pour calculer la longueur de l'arête on utilise le théorème de Pythagore dans le triangle AOS rectangle en O. Dans ce triangle on a : SA2 = SO2 + OA2.
Apothème
La hauteur du triangle isocèle qui forme chaque face s'appelle l'apothème [ SH]. Pour calculer l'apothème on utilise le théorème de Pythagore dans le triangle SAH rectangle en H.
Dans ce triangle on a : SA2 = SH2 + AH2. On peut aussi se placer dans le triangle SOH rectangle en O et dans ce cas on a :
SH2 = SO2 + OH2.
Volume et Aire
Volume :
Soit une pyramide de hauteur h dont l'aire de la base est B, son volume V est : V =(1/3)B×h .
Aire : On l'obtient en faisant aire de la base + aire des faces latérales.
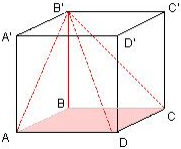
Pyramide et cube
Soit un cube ABCDA'B'C'D', dans ce cube on construit une pyramide de base, la base du cube ABCD et de sommet le point B', on obtient une pyramide de hauteur BB', une arête du cube.
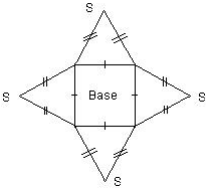
Patron d'une pyramide
Patron d'une pyramide régulière de base carrée.
Cône de révolution
Caractérisation d'un cône de révolution
Un cône de révolution est engendré par la rotation d'un triangle rectangle autour d'un des côtés de l'angle droit. Lorsqu'on fait tourner le triangle SOM autour de [SO], on obtient le cône de hauteur [SO] et de génératrice [SM]. [OM] est le rayon du cercle de base. La hauteur d'un cône de révolution est perpendiculaire à la base, donc à tout rayon de la base : [OM] ⊥ [SO].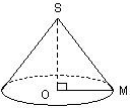 
Eléments caractéristiques d'un cône de révolution
Génératrice
La génératrice SM se calcule à l'aide du théorème de Pythagore dans le triangle SOM.
Dans ce triangle on a : SM2 = SO2 + OM2 d'où : SM2 = h2 + r2.
Volume et Aire
Volume :
Soit un cône de hauteur h dont l'aire de la base est la base est B, son volume V est : V =(1/3) B×h . Soit r le rayon de la base, on a alors B = πr2 et V = (1/3)πr2h.
Aire : On l'obtient en faisant aire de la base + aire latérale.
Aire de la base : B = πr2.
Aire latérale : c'est la surface de la portion de disque qui a pour rayon la génératrice SM du cône et pour longueur le périmètre 2πr de la base.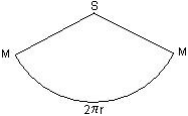 
Le disque complet a un périmètre de 2πSM et une aire de πSM2.
La portion de disque limitée par l'arc de longueur 2πr a une aire S = π×r×SM.
Cône et triangles à côtés proportionnels
Sur la figure ci-dessous les droites (HB) et (OA) sont parallèles, donc les triangles SHB et SOA sont des triangles à côtés proportionnels et on a : 
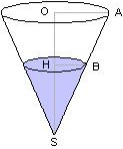
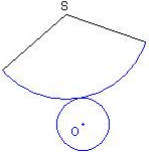
Patron d'un cône de révolution
Les longueurs tracées en bleu sont égales. 