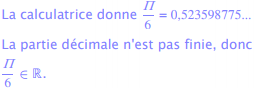Les ensembles de nombres
Définitions
Les entiers naturels ℕ
Ce sont les nombres entiers de 0 à l’infini.
ℕ = {0; 1; 2; 3; ……….}
Les entiers relatifs ℤ
Ce sont les nombres entiers de −∞ à +∞.
ℤ = { …… − 3; − 2; − 1; 0; 1; 2; 3; ……}
Les décimaux
Ils peuvent s’écrire sous la forme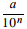 
avec a ∈ ℤ et n ∈ ℕ. Le nombre de décimales est fini.
Les rationnels ℚ
Ce sont les nombres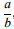 
, (a et b ∈ ℤ), dont la division « ne tombe pas juste », nombre de décimales infini.
Les réels ℝ
L’ensemble des réels contient tous les nombres précédents mais aussi tous les nombres tels que √2 ou Π
appelés irrationnels irrationnels irrationnels.
On note ℝ* l’ensemble ℝ privé de zéro et ℝ + ou ℝ − les ensembles ℝ contenant tous les nombres positifs ou négatifs. On a aussi ℝ * + et ℝ *¯.
Propriétés
ℕ ⊂ ℤ ⊂ ⊂ ℚ ⊂ ℝ
Dans ℝ on a tous les éléments de ℕ, ℤ, et ℚ.
Ecriture des nombres
Reconnaître la nature d’un nombre
Pour trouver la nature d’un nombre, on recherche le plus petit ensemble auquel il appartient.
Déterminer la nature des nombres suivants : 5,3×10−2 et 
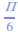
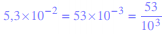
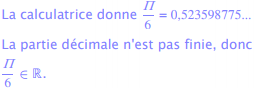
Valeurs exactes, approchées, arrondies
Valeur exacte :
, 
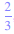
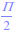
ou √7 sont des valeurs exactes.
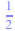
ou 0,5 sont aussi des valeurs exactes.
Valeur approchée :
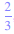
= 0,67 à 
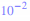
près par excès ou
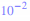
= 0,66 à près par défaut.
Valeur arrondie :
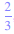
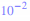
= 0,67 à près ou = 0,667 à trois chiffres significatifs.
Ordre de grandeur :
On écrit le nombre en écriture scientifique et on arrondi la partie décimale à l’entier le plus proche.
N = 6,75×10−3 or 6,75 ≃ 7, donc 7×10−3 est un ordre de grandeur de N.
Troncature :
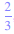
= 0,666 est une troncature à trois décimales.
Ecriture d’un calcul : ordre de priorité
Lors d’un calcul, on effectue :
- les calculs à l’intérieur des parenthèses,
- les puissances et racines carrées,
- les cosinus, sinus, …
- les multiplications et divisions dans l’ordre où elles se trouvent,
- les additions et les soustractions dans l’ordre où elles se trouvent.
Calculs et calculatrices
Saisie de nombres
On entre les chiffres qui composent le nombre et on remplace la virgule par le « point décimal ».
Taper sur la calculatrice le nombre 
:
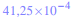
on obtient : 
Organisation des opérations
Les règles de priorité sont les mêmes que celles du calcul algébrique.
Calculer à l’aide de la calculatrice : 
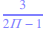
Sans les parenthèses la calculatrice effectue : 
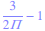
Nombres premiers
Critères de divisibilité
Soient a et b deux entiers naturels. b est un multiple de a (a est un diviseur de b) si et seulement si, il existe un entier k tel que b = ka.
b est un multiple de a.
Rechercher tous les diviseurs de 330 :
330 = 2×3×5×11
Nombres premiers
Un nombre premier est un entier naturel n’ayant que deux diviseurs 1 et lui-même.
0 et 1 ne sont pas premiers.
Décomposition en facteurs premiers
Tout entier, différent de 0 ou 1, peut se décomposer de façon unique en un produit de facteurs premiers.
Déterminer si un entier est premier :
Si n n’admet aucun diviseur premier inférieur ou égal à √n c’est qu’il est premier.