Équations
Définition
Résoudre une équation c'est trouver toutes les valeurs de la variable qui vérifient l'égalité et donner l'ensemble des solutions.
Résolution
1. Équations se ramenant à ax + b = 0 Si a ≠ 0- et b ¹ 0, la solution unique est x = -
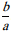
- et b = 0, la solution unique est x = 0.
- et b ≠ 0, on arrive à une impossibilité et l'équation n'a pas de solution : S = Ø.
- et b = 0, on a 0x = 0, dans ce cas il y a une infinité de solutions : S = ℝ.
Produit de facteurs
Un produit de facteurs est nul, si et seulement si, l'un de ses facteurs est nul. A*B = 0 ⇔ A = 0 ou B = 0.Quotient nul
Un quotient est nul, si et seulement si, son numérateur est nul et son dénominateur n'est pas nul. N/D = O , N = 0 et D ≠ 0.Résolution graphique
L'équation f(x) = 0 peut se résoudre graphiquement (en général de façon approchée). Les solutions sont les points d'intersection de la courbe représentative de f avec l'axe des abscisses.
L'équation f(x) = g(x) peut aussi se résoudre graphiquement. On trace les courbes représentatives Cf et Cg des fonctions f(x) et g(x). Les solutions sont les points d'intersection des courbes représentatives de f et de g. a. Résoudre graphiquement l'équation x²- 1 = 0On trace la courbe représentative Cf de la fonction f(x) = x²- 1 (soit sur la calculatrice graphique, soit manuellement). La courbe Cf coupe l'axe des abscisses en x = - 1 et x = 1, d'où les solutions de l'équation : S = {-1; 1}.
b. Résoudre graphiquement l'équation x²- 1 = x + 1 On trace la parabole f(x) = x 2 - 1 et la droite d'équation d(x) = x + 1. Ces deux courbes se coupent en x = - 1 et x = 2, d'où les solutions de l'équation : S = {-1; 2}.Inéquations
Signe de ax + b
Etudier le signe de 2x - 7 en fonction de x. 2x - 7 = 0 pour x = 7 2 Puis on dresse le tableau de signes ci-contre :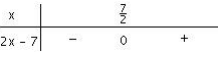
Signe d'un produit ou d'un quotient
Signe d'un produit
Etudier le signe de P( x) = ( x + 2 ) ( 3 - x) en fonction de x. ( x + 2 ) ( 3 - x) = 0 pour x + 2 = 0 ou 3 - x = 0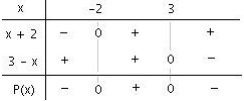
On dresse un tableau de signes et on a : P( x) < 0 pour x 2 ] -1; - 2 [⋃] 3; + 1 [
P( x) = 0 pour x = - 2 ou x = 3;
P( x) > 0 pour x 2 ] -2; 3 [
Signe d'un quotient
La méthode est identique dans le cas d'un quotient, il faut cependant ajouter une condition, le terme au dénominateur ne doit pas être nul.
Etudier le signe de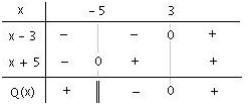
en fonction de x. On calcule la valeur interdite :
x + 5 = 0, soit x = - 5.
Cette valeur est représentée dans le tableau par une double barre verticale.
Q(x) ≤ 0 pour x 2 ] -5; 3 ] 
Q(x) ≥ 0 pour x 2 ] -1; - 5 [⋃[ 3; + 1 [
Résoudre une inéquation
Pour résoudre une inéquation on se ramène à une comparaison à 0. Pour résoudre A(x) ≥ B(x), on résout A(x) - B(x) ≥ 0. Résoudre l'inéquation x3 - 2x2 + 5x + 1 > 5x + 1. x3 - 2x2 + 5x + 1 > 5x + 1 ⇔ x3 - 2x2 + 5x + 1 - 5x - 1 > 0 ⇔ x3 - 2x2 > 0 ⇔x2( x - 2 ) > 0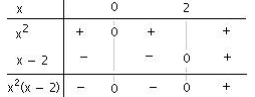
On lit le résultat dans le tableau de signes :
x2( x - 2 ) > 0 pour x > 2, d'où : S = ] 2; + 1 [