Angles inscrits-Angles au centre
Définition
Angle inscrit : c'est un angle dont le sommet est sur un cercle et dont les côtés sont des cordes Angle inscrit de ce cercle.
Angle au centre : c'est un angle dont le sommet est le centre du cercle et dont les côtés sont Angle au centre des rayons du cercle.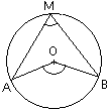 
Corde : c'est un segment qui joint deux points distincts du cercle.
[AM] et [BM] sont des cordes, [AB] est aussi une corde.
Propriétés
Dans un même cercle ou dans deux cercles de même rayon deux angles au centre égaux interceptent des arcs égaux.
Et réciproquement réciproquement réciproquement :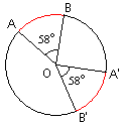 
Deux arcs égaux sont interceptés par des angles au centre égaux.
et réciproquement.
Dans un même cercle ou dans deux cercles de même rayon deux angles inscrits égaux interceptent des arcs égaux.
Et réciproquement :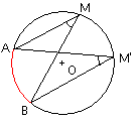 
Deux arcs égaux sont interceptés par des angles inscrits égaux.
car ils n'interceptent pas le même arc :
l'angle 
intercepte l'arc 
,
l'angle 
intercepte l'arc 
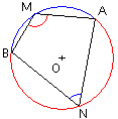
: ce sont des angles supplémentaires.
Théorème de l'angle au centre
Dans un cercle un angle inscrit est égal à la moitié de l'angle au centre qui intercepte le même arc.
= (1/2) 
ou =2 
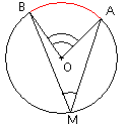
Dans le cas où [AB] est un diamètre, on retrouve un résultat déjà connu. Un triangle rectangle est inscrit dans un demi-cercle dont le diamètre est l'hypoténuse du triangle.
Rotations
Définition
L'image d'un point M (autre que O) dans la rotation de centre O et d'angle α est le point M ' tel que : OM = OM' et 
=α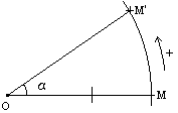 
Les points M et M ' sont sur le cercle de centre O et de rayon OM. Le point O est sa propre image.
On défini un sens positif (direct) des rotations : le sens inverse des aiguilles d'une montre.
Propriétés
La rotation conserve :
- l'alignement des points,
- les longueurs, les angles , les aires,
- le parallélisme, l'orthogonalité.
Image d'une figure
Le triangle rectangle ABC est transformé en un triangle rectangle A'B'C' dans la rotation de centre O et d'angle α.
Les triangles ABC et A'B'C' ont les mêmes dimensions : ils sont superposables.
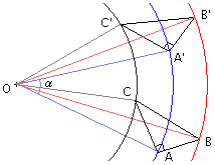
- Un segment segment segment a pour image un segment de même longueur.
- Une droite D a pour image une droite D'. Deux cas :
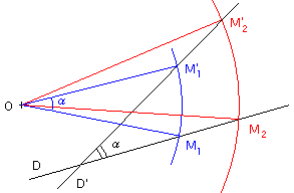
Le point O n'appartient pas à la droite D: les droites D et D' se coupent en faisant un angle α (égal à l'angle de rotation) entre elles.
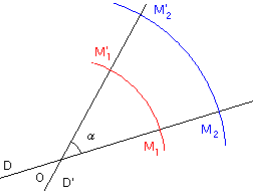
Le point O appartient à la droite D: les droites D et D' se coupent en O en faisant un angle α (angle de rotation) entre elles.
- Le cercle de centre I a pour image le cercle de centre I ' où I ' est l'image du point I dans la rotation de centre O et d'angle α.
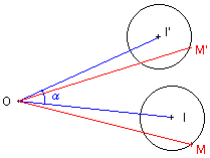
Les deux cercles ont même rayon IM = I 'M '. Le cercle de centre O a pour image lui-même dans la rotation de centre O.
Polygones réguliers
Définition
Un polygone régulier est un polygone ayant des côtés de même longueur et des angles égaux.
Propriétés
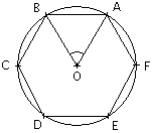
Tout polygone régulier s'inscrit dans un cercle dont le centre est le centre du polygone.
Chaque sommet est obtenu comme image du sommet qui le précède par la rotation de centre O et d'angle . Cette rotation transforme le polygone régulier en lui-même.Un polygone régulier est un polygone tel qu'il existe une rotation qui le laisse invariant.
Conséquences
Tous ses sommets sont situés sur un cercle dont le centre est le centre de la rotation, c'est aussi le centre du polygone.
La mesure de l'angle au centre d'un polygone de n côtés est : 
en degrés.
Un hexagone régulier est constitué de six triangles équilatéraux de côtés R, rayon du cercle circonscrit. Les autres polygones réguliers se divisent en triangles isocèles de sommet O.
Cercle inscrit
Les milieux des côtés d'un polygone régulier convexe appartiennent à un même cercle tangent aux côtés du polygone : c'est le cercle inscrit.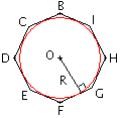 
Le rayon R de ce cercle est l'apothème apothème apothème du polygone.