Théorème de Pythagore
Enoncé du théorème
Soit le triangle ABC rectangle en A on a : 
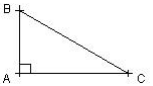
Calculer la longueur de l'hypoténuse
Soit le triangle ABC rectangle en A tel que AB = 9 cm et AC = 12 cm. Calculer BC. Le triangle ABC est rectangle, donc on utilise le théorème de Pythagore :
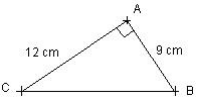
BC = √225 = 15 cm.
Calcul de la longueur d'un des côtés de l'angle droit
Soit le triangle DEF rectangle en D tel que DE = 5 cm et EF = 11 cm. Calculer DF. Le triangle DEF est rectangle, donc on applique le théorème de Pythagore
,
soit DF = 96 p ' 9,8 cm arrondi au millimètre. 
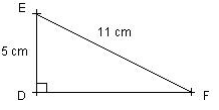
Réciproque du théorème de Pythagore
Si dans le triangle ABC on a 
, alors ce triangle est rectangle en A et BC est son hypoténuse.
Démontrer qu'un triangle est rectangle
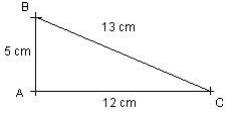
Soit le triangle ABC tel que AB = 5 cm, AC = 12 cm et BC = 13 cm.
Démontrer que ABC est rectangle. On calcule le carré de chacun des côtés : 
,
. 
On fait la somme des deux plus petits : 
.
Or on a 
, donc 
.
D'après la réciproque du théorème de Pythagore : le triangle ABC est rectangle en A .
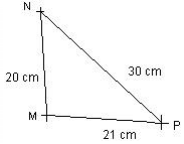
Soit le triangle MNP tel que MN = 20 cm, MP = 21 cm et NP = 30 cm.
Le triangle MNP est-il rectangle ?
On calcule le carré de chacun des côtés : 
et 
`
On fait la somme des deux plus petits : 
Or on a 
D'après la réciproque du théorème de Pythagore le triangle MNP n'est pas rectangle.
Cosinus
Définition
Pour chaque angle aigu a d'un triangle rectangle, on appelle cosinus α le nombre
. 
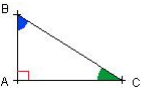
Dans le triangle ABC ci-contre on a 
Déterminer un cosinus ou un angle à la calculatrice
La touche 
de la calculatrice donne une valeur approchée du cosinus d'un angle.
La touche 
de la calculatrice donne une valeur approchée d'un angle dont on connaît le cosinus.
Déterminer un angle aigu dans un triangle rectangle
Soit le triangle ABC rectangle en A tel que AB = 2 cm et BC = 5 cm. Calculer 
(arrondir au degré).
Le triangle ABC est rectangle, donc on a :
La calculatrice donne 
Calculer les côtés d'un triangle rectangle
Calculer l'arrondi au millimètre près de la longueur du côté [ AB] du triangle
ABC tel que BC = 3 cm et 
On connaît l'angle 
et l'hypoténuse, donc on a :
. 
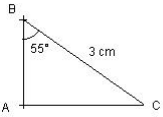
La calculatrice affiche : 1,720729309, donc : AB ≈ 1,7 cm arrondi au mm.
Triangles à côtés proportionnels
Les cosinus des angles aigus de deux triangles à côtés proportionnels sont égaux entre eux.
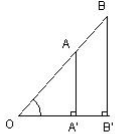
Cercle trigonométrique
Soit dans un repère orthonormé le quart de cercle de centre O et de rayon 1. Soit le point M appartenant à ce cercle, le point M a pour abscisse OM ' = x.
Le triangle MOM ' est rectangle en M ' et on a : 
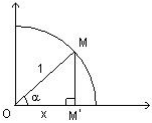
Le cosinus de l'angle α est l'abscisse du point M.