Fonctions linéaires-Fonctions affines

Fonction linéaire

Définition

Soit un nombre a donné, la relation qui, à tout x associe y tel que y = ax est une fonction linéaire.

On la note : x ↦ ax ou encore f( x) = ax. On a une relation de proportionnalité entre x et y.

Représentation graphique

La représentation graphique d'une fonction linéaire est une droite passant par l'origine : y = ax. a est le coefficient directeur ou pente de la droite, c'est aussi le coefficient de proportionnalité de la fonction.

Détermination d'une fonction linéaire

Une fonction linéaire est déterminée par son coefficient de proportionnalité a.

Déterminer la fonction linéaire f telle que f(2) = 5.

Soit a le coefficient de la fonction f(x) = ax, on a f(2) = 2a

Or f(2) = 5 donc pour trouver a il suffit de résoudre l'équation 2a = 5, d'où : a =(5/2)

et la fonction recherchée est :  f ( x ) =(5/2)x.

 

Exemples de fonctions linéaires

Vitesse

L'expression donnant la distance d parcourue pendant un temps t à la vitesse constante v est donnée par :

d = vt est une fonction linéaire. Le coefficient de proportionnalité est la vitesse v.

Un cycliste roule à 10 km/h, on a : d = 10t

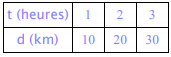
Il y a proportionnalité entre la distance parcourue et le temps.

Le coefficient de proportionnalité : 10 est égal à la vitesse du cycliste.

Conversions

Soit x la somme en euros et y la même somme en francs. Sachant que 1 euro vaut 6,50 francs donner la relation qui permet de convertir en francs.

On a y = 6,50x qui est une fonction linéaire dont le coefficient de proportionnalité est 6,50 Pour x = 1 (1 euro) y = 6,50 (6,50 francs) Pour x = 2 (2 euro) y = 13 (13 francs)

Augmentation - Diminution

Soit x le prix initial et y le prix après augmentation. On fait une augmentation de 10%, on a :

Le coefficient de proportionnalité est ici égal à  ou encore 1,10.

Soit x le prix initial et y le prix réduit. On fait une réduction de 15%, on a :

On a une fonction linéaire dont le coefficient de proportionnalité est  soit 0,85.

Dans le cas d'une augmentation de prix le coefficient de proportionnalité est supérieur à 1.

Dans le cas d'une diminution de prix le coefficient de proportionnalité est inférieur à 1.

Fonctions affines

Définition

Soient deux constantes a et b, la relation qui à tout x associe y tel que y = ax + b est une fonction affine. On la note : x↦ ax + b ou encore f(x) = ax + b

Représentation graphique

La représentation graphique d'une fonction affine est une droite ne passant pas par l'origine. La constante b se retrouve graphiquement, c'est l'ordonnée à l'origine c'est à dire la valeur que prend f(x) lorsque x est nul : f(0) = b.

Détermination d'une fonction affine

Pour connaître une fonction affine il suffit de connaître ses deux constantes a et b. Soit la fonction affine f(x)=ax+b et f(x₁) = y₁ et f(x₂) = y2 x₁, x₂, y₁ et y₂ des réels donnés.

Pour trouver a et b il suffit de résoudre le système :  d'où   ou encore y₂ - y₁ = a(x₁ - x2)

Cela signifie qu'il y a proportionnalité des accroissements de x et de y.

Soit la fonction affine f(x) = 2x + 3.

Si l'accroissement des x est 1 alors l'accroissement des y correspondant sera :

2×1 = 2.

Vérification :

Soit x₁= 1 et x2= 2 (on a bien x2 - x₁= 1) y₂ = f(x2) = 2×2 + 3 = 7 y₁ = f(x₁) = 2×1 + 3 = 5 d'où l'accroissement des y : y₂ - y₁ = 7 - 5 = 2 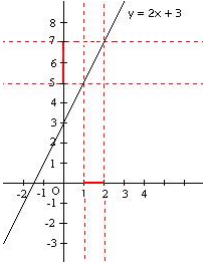                   Sur la représentation graphique on lit : à un accroissement d'une unité sur l'axe des x correspond un accroissement de deux unités sur l'axe des y.