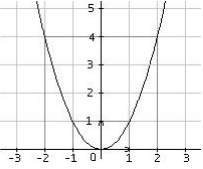
Fonction carrée x ↦ x²
La fonction carrée est définie sur l'ensemble des réels ℝ par f( x) = x². C'est une fonction paire : f( -x) = f( x). Sa courbe représentative appelée parabole est symétrique par rapport à l'axe des ordonnées.
Fonction inverse x ↦
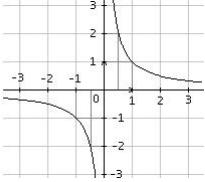
La fonction inverse est définie sur ] -1; 0 [[ ] 0; + 1 [ par f( x) =
C'est une fonction impaire f(-x) = - f(x). Sa courbe représentative appelée hyperbole est symétrique par rapport à l'origine O( 0; 0 ) du repère. Les axes du repère sont appelés asymptotes à la courbe.
Les axes du repère sont appelés asymptotes à la courb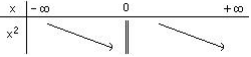e.
La double barre dans le tableau ci-dessus indique que la valeur x = 0 est une valeur interdite.
Fonctions cosinus et sinus
Définition
Soit dans un repère (O ; I ; J ) orthonormal, le cercle trigonométrique de centre O et de rayon 1. Tout point M du cercle a pour abscisse cos x et pour ordonnée sin x. Lorsque le point M se déplace sur ce cercle, les valeurs de cos x et sin x varient en fonction des valeurs de l'angle x.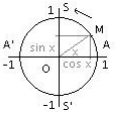 
Sens de variation
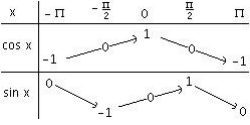
On étudie les variations des fonctions cos x et sin x. Les fonction cosinus et sinus sont des fonctions périodiques. On trace le tableau de variations sur un intervalle de longueur 2π, soit entre -π et π . Ce qui correspond sur le cercle trigonométrique à un déplacement du point M de A' en A'. On obtient le tableau ci-contre.
Représentation graphique
Contrairement à la représentation graphique d’une fonction linéaire qui est une droite, les courbes représentatives des fonctions cosinus et sinus sont des sinusoïdes. La fonction cosinus est une fonction paire, sa courbe représentative est symétrique par rapport à l'axe des ordonnées et on a cos (-x) = cos x. La fonction sinus est une fonction impaire, sa courbe représentative est symétrique par rapport à l'origine du repère et on a sin(-x)=-sinx.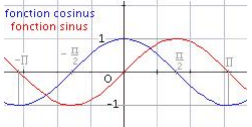
Autres fonctions de référence
Fonction racine carrée x ↦ √x
La fonction racine carrée est définie sur [ 0; + 1 [ par f( x) =√x. La fonction carrée est strictement croissante sur ℝ+ . La fonction racine carrée n'est ni paire ni impaire. Sa courbe représentative est donnée sur la figure ci-contre.
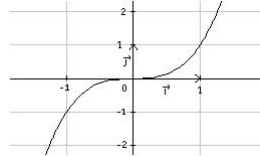
Fonction cube x ↦ x³
La fonction cube est définie sur ℝ par f( x) = x. La fonction cube est strictement croissante sur ℝ. La fonction cube est impaire : f( -x) = ( -x)³ = - x³ = - f( x). Sa courbe représentative est donnée sur la figure ci-contre.
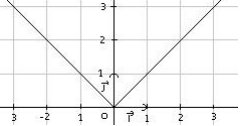
Fonction valeur absolue x ↦ |x|
La fonction valeur absolue est définie sur ℝ par f(x) = |x|. La fonction valeur absolue est paire : f(-x) = |- x| = |x|. La courbe représentative de f est formée de la demi-droite d'équation y = x sur [ 0; + 1 [ et de la demi-droite d'équation y = - x sur [ -1; 0 [ . Sa courbe représentative est donnée sur la figure ci-contre.
